Gaußsche Normalverteilung - ein Würfelexperiment

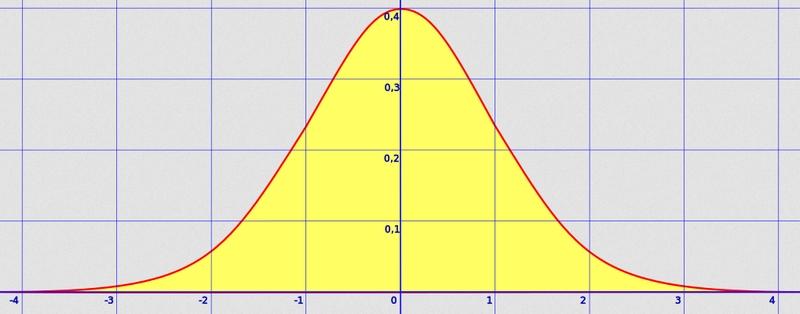
Die Normalverteilung - auch Gaußsche (Normal)Verteilung genannt - ist die wichtigste Wahrscheinlichkeitsverteilung und nimmt bei unzähligen statistischen Analysen eine tragende Rolle ein. In der Praxis wird die Normalverteilung in zahlreichen Datenauswertungen angewandt.

Anwendung findet die Normalverteilung auch in vielen Fällen in der Naturwissenschaft wie z.B. Biologie (Körpergröße, Blutdruck), Physik (Messfehler), Meteorologie (Regenmenge, Sonnenstunden).

Grund genug also, sich des Themas Normalverteilung auch im Informatikunterricht in Kombination mit Mathematik anzunehmen und den Schüler*innen so einen neuen Zugang zu eröffnen.

Wahrscheinlichkeitsverteilungen sind nützlich, wenn man für ein Zufallsereignis wissen möchte, welche Ergebnisse am wahrscheinlichsten sind. Das erprobten die Schüler*innen mit Hilfe von 2 Spielwürfeln. Sie schätzten zunächst, welche Zahl nach insgesamt 3 gespielten Runden pro Schüler*in am häufigsten vorkommen wird.

Für einen einzelnen Würfel ist die Chance für eine 1-2-3-4-5-6 identisch. Verwendet man aber 2 Würfel und addiert die Augenzahlen, so besteht eine Wahrscheinlichkeit von 1/36, dass die Summe 2 ergibt. Um eine 3 zu erhalten hat man eine Wahrscheinlichkeit von 2/36, für eine 4 von 3/36. Die Wahrscheinlichkeit nimmt zu, da mit höherer Zahl mehrere Kombinationen möglich sind, bis mit 6/36 die Wahrscheinlichkeit eine 7 zu erhalten, am höchsten ist (1+6 / 6+1 / 2+5 / 5+2 / 3+4 / 4+3)

Dann nimmt die Wahrscheinlichkeit wieder ab, bis für die 12 wieder eine Wahrscheinlichkeit von 1/36 vorliegt.

Würde sich nach 3 Durchgängen (insgesamt 45 Würfen) bereits eine Normalverteilung aufgrund der Wahrscheinlichkeit erkennen lassen, oder würde das Ergebnis vollständig anders aussehen?

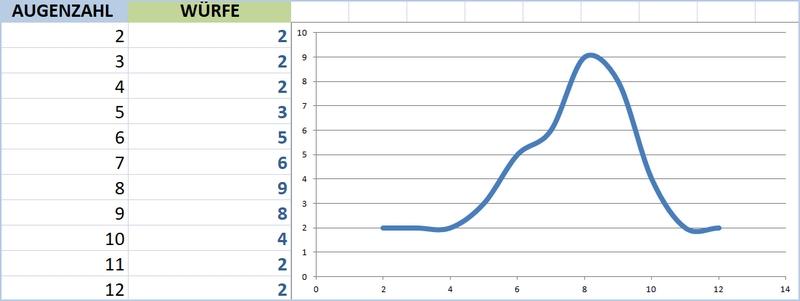
Das Experiment konnte beginnnen und die Schüler*innen notierten gemeinsam jeden einzelnen Wurf in einer Excel-Tabelle. Auch wenn nach 3 Runden mit 45 Würfen nicht die Zahl 7 am häufigsten vorkam, so war doch bereits die Normalverteilung zu erahnen.

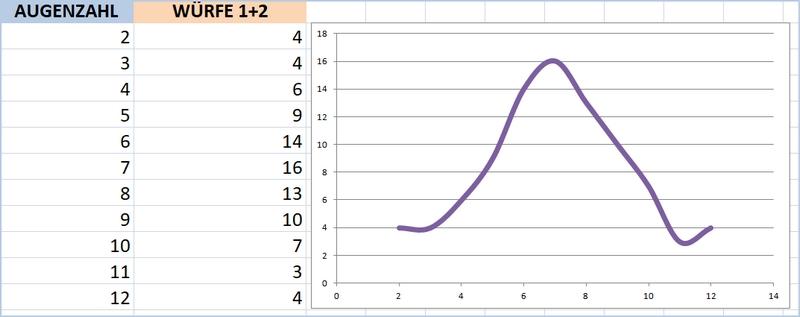
Wie würde sich das Ergebnis verändern, wenn noch einmal 3 Runden gewürfelt wird? Die Schüler*innen gaben erneut ihre Einschätzungen ab und dann ging es auch schon an die weiteren Wurfergebnisse. Und nach insgesamt 6 Durchgängen mit 90 Würfen in Summe sah die Verteilung bereits viel deutlicher aus.

Auf diese Weise erschloss sich den Schüler*innen das Thema Normalverteilung und Wahrscheinlichkeit sehr anschaulich. Würde man nun noch zusätzlich weitere Runden spielen und die Anzahl der Würfe erhöhen, dann werden die Grenzfälle immer unwahrscheinlicher und man hätte letztendlich eine Glockenkurve.